1. 주택 임대료 예측 데이터셋
House Rent Prediction Dataset은 주택 임대료를 예측하기 위한 목적으로 사용되는 데이터셋입니다. 이 데이터셋은 주로 머신러닝 및 데이터 분석 프로젝트에서 사용되며, 주택의 다양한 특성과 위치 정보를 기반으로 임대료를 예측하는 모델을 학습하는 데 활용됩니다.
House Rent Prediction Dataset
Renting Insights: House Rent Prediction Dataset with 4700+ Listings
www.kaggle.com
2. 데이터셋 컬럼
- BHK: 주택에 포함된 침실, 거실, 주방의 총 개수를 의미합니다.
- Rent: 주택(아파트/플랫)의 월 임대료를 나타냅니다.(이걸 예측해야하니 이걸 종속변수로)
- Size: 주택(아파트/플랫)의 면적을 평방피트(Square Feet)로 나타냅니다.
- Floor: 주택이 위치한 층수와 건물의 총 층수를 나타냅니다. (예: 2층 중 1층, 5층 중 3층 등)
- Area Type: 주택의 면적이 어떤 방식으로 계산되었는지를 나타냅니다. (예: 전체 면적, 실사용 면적, 건축 면적 등)
- Area Locality: 주택(아파트/플랫)이 위치한 구체적인 지역이나 동네 정보를 나타냅니다.
- City: 주택(아파트/플랫)이 위치한 도시를 나타냅니다.
- Furnishing Status: 주택이 가구가 완비되었는지(Furnished), 부분적으로 갖추어졌는지(Semi-Furnished), 아니면 비어 있는지(Unfurnished)를 나타냅니다.
- Tenant Preferred: 집주인 또는 중개인이 선호하는 임차인 유형을 나타냅니다. (예: 가족, 싱글, 직장인 등)
- Bathroom: 주택에 있는 욕실의 개수를 나타냅니다.
- Point of Contact: 주택(아파트/플랫)에 대한 추가 정보를 얻기 위해 연락해야 할 담당자나 중개인의 정보를 나타냅니다.
3. 데이터셋 전처리
1. 라이브러리 불러오기
먼저, 필요한 라이브러리를 불러옵니다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
- pandas 및 numpy: 데이터 처리 및 분석
- matplotlib.pyplot 및 seaborn: 데이터 시각화
- sklearn.model_selection: 데이터 분할
- sklearn.preprocessing: 범주형 데이터 인코딩
- sklearn.linear_model: 선형 회귀 모델
- sklearn.metrics: 모델 평가 지표
rent_df = pd.read_csv('내드라이브 경로/House_Rent_Dataset.csv')
rent_dfCSV 파일을 불러와 DataFrame으로 저장합니다.

rent_df.info()데이터셋의 컬럼, 데이터 타입, 결측값을 확인합니다.

info로 보면 null값을 없다는 것을 일단 확인 할 수 있습니다
rent_df.describe()수치형 변수의 통계를 요약 확인합니다

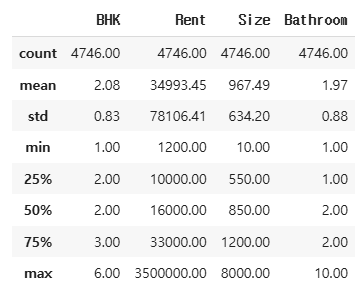
round(rent_df.describe(), 2)좀 더 보기 편하도록 소수점 둘째 자리 까지만 통계를 확인합니다
데이터 분포도 확인
displot을 사용해 히스토그램을 이용해서 각 변수들의 데이터 분포도를 시각화하여 확인해보자
sns.displot(rent_df['BHK'])
sns.displot(rent_df['Rent'])
렌트비용에 대한 히스토그램을 확인해보니 한곳에만 비용의 분포도가 몰려있고 최대값과 차이가 있다.
이 경우에는 이 최대값이 결측지에 해당할지에 대한 분석을 통해서 결측지로 판단 후 이 데이터를 없앨 것인지 판단이 필요하다.
rent_df['Rent'].sort_values()
sort를 통해서 순서대로 정렬해서 rent를 확인해 보니 제일 작은 가격이 1200 제일 큰 가격은 3500000이다
가격차이가 있기는 하지만 데이터 삭제는 신중해야 하므로 다른 변수도 마저 시각화 하겠다
sns.displot(rent_df['Size'])
렌트하는 방의 사이즈도 한쪽에 데이터가 좀 몰려있으며 최대값과 차이가 나는것을 확인 할 수 있다 결측지 인지 판단이 필요할 것 같다
boxplot
Boxplot은 데이터의 중앙값, 사분위수, 이상치 등을 시각적으로 표현하는 통계 그래프입니다. 주로 데이터 분포와 이상치를 빠르게 파악하기 위해 사용됩니다.
- 중앙값 (Median, Q2): 데이터를 크기 순으로 정렬했을 때 중간에 위치한 값
- Q1 (제1사분위수, 25%): 하위 25%에 해당하는 값
- Q3 (제3사분위수, 75%): 상위 25%에 해당하는 값
- IQR (Interquartile Range, 사분위 범위): Q3 - Q1, IQR은 데이터의 중간 50% 범위를 의미합니다.
- Minimum: Q1 − 1.5 × IQR 이하에 속하지 않는 가장 작은 값
- Maximum: Q3 + 1.5 × IQR 이하에 속하지 않는 가장 큰 값
- 이상치: 일반적인 데이터 분포를 벗어난 값(Lower Bound=Q1−1.5×IQR, Upper Bound=Q3+1.5×IQR)
- IQR 기준으로 이상치를 정의하기 때문에 모든 상황에 완벽하지 않을 수 있습니다
boxplot은 데이터 분석 과정에서 가장 많이 사용하는 시각화 방법으로 원래 이름은 상자수염 도표(Box-and-Whisker-Plot)이라고 불리운다.
boxplot은 데이터셋의 분포와 변동성을 한눈에 시각화 하기에 좋다.
boxplot은 아래와 같은 구성 요소로 구성된다.
boxplot은 주로 IQR을 기반으로 본다. 통계적인 이야기를 할때는 IQR이라는 용어를 많이 사용하는데.예를 들어 데이터를 제외할때 "IQR 몇으로 제외했어요?"로 묻는 식이다.
여기서 IQR(사분위수 범위)은 데이터를 사분위수로 나누어 표시하는것이다.
사분위수는 순위가 매겨진 데이터를 4개의 동일한 부분으로 나눈다. 중요한 것은 최소 및 최대값에 대해 어떻게 할 것인가이다.
여기서 데이터분포에 따라 다양한 측면을 IQR의 특정 배수로 확장 될 수 있다.
그렇다면 무조건 1.5배가 답이 되지는 않는다는 이야기이다. 배수를 조정해 가면 해당 데이터셋의 분포에 가장 적합한 배수를 정해야 한다는 이야기이다. 박스플롯 시각화만으로도 데이터에 대한 많은 특성을 알 수 있다.


결측지 판단을 위해서 boxplot을 사용해 보도록하자
sns.boxplot(rent_df['Rent'])
sns.boxplot(rent_df['Size'])
sns.boxplot(rent_df['BHK'])
boxplot 해석
박스플롯은 데이터의 중심 경향과 확산을 분석 할 수 있다. 중앙값(상자 안의 선) 은 데이터셋의 중간값을 나타내며. 상자의 길이(IQR)는 중간 50%이내의 데이터 변동성을 나타낸다. 수염은 사분위수를 넘어서는 데이터 범위에 대한 정보를 제공한다.
또 하나는 이상치를 찾아 볼수 있다. 이상값은 상자 그림의 수염 외부에 있는 개별 게이터 포인트이다. 이는 데이터셋의 비정상적이거나 극단적인 값을 나타낸다.
박스플롯에서 얻어낸 인사이트를 활용하여 데이터 분포에 대한 결론을 도출할 수 있다.
패턴이나 추세를 파악하고,데이터 분석을 기반으로 의사결정을 내리게 된다. 분포가 대칭인지 치우친 것인지, 해석에 영향을 미치는 이상값이 있는지, 여러 그룹이나 범주에서 데이터가 어떻게 비교되는지 따져 봐야 한다.
박스플롯 해석 시 아웃라이어라고 반드시 다 결측지로 보고 삭제를 하는것 또한 데이터 분석 방향성과 목적에 따라 다를 수 있다. 해서 아웃라이어라고 해도 데이터의 유형과 분석 방향성에 대해 생각 후 적절히 처리하는 것이 중요하다.
범주형 변수 확인
rent_df['Area Type'].unique()
- unique(): Area Type 컬럼에 포함된 서로 다른 값(범주형 변수의 종류)을 확인합니다.
rent_df['Area Type'].nunique()
#3- nunique(): Area Type 컬럼의 고유한 개수를 확인하여 범주형 변수인지 파악합니다.
for i in ['Floor', 'Area Type', 'Area Locality', 'City', 'Furnishing Status', 'Tenant Preferred', 'Point of Contact']:
print(i, rent_df[i].nunique())
- for 루프를 사용하여 특정 컬럼들을 하나씩 반복 처리합니다.
- rent_df[i].nunique(): i에 해당하는 컬럼의 고유한(unique) 값의 개수를 출력합니다.
- 결과적으로, 데이터셋의 범주형(카테고리형) 변수들이 몇 개의 서로 다른 값을 가지고 있는지 확인하는 과정입니다.
- 범주형 변수 인코딩 여부를 결정하기 위해:
- 범주형 데이터가 너무 많은 고유 값을 가지면, 머신러닝 모델에서 적절히 처리하기 어려울 수 있습니다.
- 예를 들어, Area Locality 컬럼이 수천 개의 고유 값을 가진다면 이를 그대로 사용할 경우 모델 학습이 어려워질 수 있습니다.
- 반면, Furnishing Status와 같은 변수는 고유 값이 3개 (예: Furnished, Semi-Furnished, Unfurnished) 정도로 작다면 원-핫 인코딩 또는 라벨 인코딩을 통해 처리 가능합니다.
- 불필요한 변수 제거를 결정하기 위해:
- Floor나 Area Locality가 너무 많은 범주를 가지고 있다면 모델 성능에 부정적인 영향을 미칠 가능성이 있습니다.
- City, Furnishing Status, Tenant Preferred, Point of Contact는 범주형 데이터로서 머신러닝 모델에 사용할 수 있도록 변환해야 합니다.
rent_df.drop(['Floor', 'Area Locality', 'Posted On'], axis=1, inplace=True)
- Floor: 층 정보를 포함하지만, 모델 예측에 큰 영향을 주지 않을 가능성이 높아 제거합니다.
- Area Locality: 특정 지역명을 포함하는 컬럼으로, 너무 많은 고유 값이 존재하여 예측에 적절하지 않을 수 있어 제거합니다.
- Posted On: 날짜 정보는 모델 학습에 직접적인 영향을 주지 않을 것으로 판단되어 제거합니다.
rent_df = pd.get_dummies(rent_df, columns=['Area Type', 'City', 'Furnishing Status', 'Tenant Preferred', 'Point of Contact'])
rent_df.head()이 코드는 pandas의 get_dummies() 함수를 사용하여 범주형(Categorical) 데이터를 원-핫 인코딩(One-Hot Encoding)하는 과정이다.
- pd.get_dummies()는 문자열 데이터를 숫자 데이터(0과 1)로 변환하는 기능을 한다.
- 머신러닝 모델은 일반적으로 숫자 데이터를 다루므로, 범주형 데이터(카테고리형 변수)를 원-핫 인코딩해야 한다.

X = rent_df.drop('Rent', axis=1) # 독립변수
y = rent_df['Rent'] # 종속변수독립변수와 종속변수를 변수에 저장해준다.
X.head()
y.head()
from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.3,
random_state=2025)학습 데이터와 테스트 데이터를 분리해준다
X_train.shape,X_test.shape
# ((3322, 21), (1424, 21))y_train.shape,y_test.shape
# ((3322,), (1424,))4. 알고리즘으로 모델링
※ 선형 회귀
선형 회귀(Linear Regression)는 독립 변수(Feature)와 종속 변수(Target) 간의 선형적 관계(Linear Relationship)를 찾아내어 예측을 수행하는 통계적 모델입니다. 주어진 데이터를 통해 최적의 직선(회귀선, Regression Line)을 찾아내며, 이 직선은 데이터 포인트와의 오차(Residuals)를 최소화하는 방향으로 설정됩니다. 수식으로는 y=wx+b로 표현되며, 여기서 w는 기울기(Weight), b는 절편(Bias)입니다. 주로 수식적 최적화(일반 최소제곱법, OLS)를 통해 학습되며, 해석이 명확하고 계산이 효율적이라는 장점이 있습니다.
※ 최소 제곱법
최소 제곱법(Least Squares Method)은 주어진 데이터 포인트들과 예측 모델(주로 직선) 사이의 오차(Residuals)의 제곱합(Sum of Squared Errors, SSE)을 최소화하여 최적의 예측 모델을 찾아내는 통계적 방법입니다. 이 방법은 선형 회귀 분석에서 가장 널리 사용되며, 데이터 포인트들이 회귀선(Regression Line)에 최대한 가깝도록 조정합니다. 수학적으로는 오차의 제곱합을 최소화하는 기울기(w)와 절편(b)을 계산하여 모델을 최적화합니다.

선형 회귀 모델 학습 및 예측
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train, y_train) # 모델 학습
pred = lr.predict(X_test) # 예측값 생성
- LinearRegression() 객체를 생성하여 lr에 저장
- lr.fit(X_train, y_train): 훈련 데이터(X_train, y_train)를 사용하여 선형 회귀 모델을 학습
- lr.predict(X_test): 학습된 모델을 사용하여 X_test에 대한 예측값(pred) 생성
모델 평가 지표 계산
from sklearn.metrics import mean_squared_error, root_mean_squared_error
print(mean_squared_error(y_test, pred))
print(root_mean_squared_error(y_test, pred))
# 1845945611.7086728
# 42964.46917755034
- 평균 제곱 오차(MSE, Mean Squared Error): 예측값과 실제값 간의 차이를 제곱하여 평균을 낸 값. 값이 작을수록 모델이 더 정확함.
- 평균 제곱근 오차(RMSE, Root Mean Squared Error): MSE의 제곱근을 취한 값으로, 실제 데이터와 단위가 같아 해석이 용이함.
오차값이 너무 크다 데이터 처리를 좀 더 해서 개선해 보도록 하자
특정 데이터 확인
X_train.loc[1837] # X_train에서 1837번째 데이터 확인
y_train.loc[1837] # y_train에서 1837번째 데이터 확인


- X_train.loc[1837]: 훈련 데이터의 1837번째 샘플 확인
- y_train.loc[1837]: 해당 샘플의 타깃 값 확인
- → 이 과정에서 이상치(outlier) 여부를 판단
아웃라이어 제거
X_train.drop(1837, inplace=True)
y_train.drop(1837, inplace=True)
- drop(1837, inplace=True): 1837번째 데이터 샘플을 삭제
- inplace=True: 원본 X_train과 y_train이 변경됨 (새로운 변수에 저장하지 않고 직접 수정)
lr = LinearRegression()
lr.fit(X_train, y_train)
new_pred = lr.predict(X_test)
root_mean_squared_error(y_test, new_pred)
- 이상치 제거 후 새로운 모델(lr)을 다시 학습
- 새로운 예측값(new_pred)을 생성
# pred - new_pred
42964.46917755034 - 42987.37959096641
이상치 제거 전후의 예측값 차이 확인
결과적으로 이상치를 제거한 후 RMSE가 크게 변하지 않았으므로, 해당 데이터가 모델 성능에 큰 영향을 주지 않았을 가능성이 큼.
5. 로그 변환으로 RMSE 개선
주택 임대료 데이터셋은 오른쪽으로 치우친 분포를 가지고 있습니다. 값이 큰 임대료(Outliers)가 평균과 모델 예측 결과에 큰 영향을 미치기 때문에 로그 변환을 통해 값의 범위를 축소하고, 분포를 정규 분포(Normal Distribution)에 가깝게 만듭니다. 로그 변환은 극단적으로 높은 값의 영향을 줄여주기 때문에 모델이 이상치에 덜 민감하게 반응하고 RMSE가 감소할 수 있습니다.
※ 정규 분포
정규 분포(Normal Distribution)는 데이터가 평균을 중심으로 좌우 대칭을 이루며 종 모양(Bell Curve)으로 퍼져 있는 통계적 분포입니다. 대부분의 값은 평균 근처에 몰려 있고, 평균에서 멀어질수록 값의 빈도가 급격히 감소합니다. 이는 자연현상, 시험 점수, 사람들의 키와 같은 많은 실제 데이터에서 흔하게 나타납니다.
※ 데이터 변환의 개념
원본 데이터: 실제 관측된 값 그대로입니다. (예: 임대료 1,000원, 10,000원, 100,000원)
로그 변환된 데이터: 데이터의 비율(비율적 차이)에 초점을 맞추어 변환된 값입니다. (예: log(1,000) → 3, log(10,000) → 4, log(100,000) → 5)
데이터의 '값'은 변하지만, '관계'는 변하지 않습니다. 모델 학습은 변환된 데이터로 진행하지만, 최종 예측값은 원래 스케일로 되돌립니다. 변환된 데이터는 이상치를 줄이고, 정규 분포에 가깝게 만들어 모델 성능을 개선합니다.
y_train = np.log1p(y_train)
y_test = np.log1p(y_test)
lr = LinearRegression()
lr.fit(X_train, y_train)
y_pred_log = lr.predict(X_test)
#로그 예측값을 원래 값으로 변환
log_pred = np.expm1(y_pred_log)
y_test_original = np.expm1(y_test)
#성능 평가 (RMSE 계산) y_test_original: 실제 값 (로그 변환 후 복원된 값) log_pred: 예측 값 (로그 변환 후 복원된 값)
#RMSE (Root Mean Squared Error):
# 예측값과 실제값 간의 오차를 제곱, 평균낸 뒤 제곱근을 구합니다.
# RMSE는 값이 작을수록 모델의 성능이 더 좋다는 의미입니다.
root_mean_squared_error(y_test_original, log_pred)
# 결과 : 33187.45360971534np.log1p(x):
- log1p(x) = log(1 + x), 즉 로그 변환을 적용하면서 작은 값이 0에 수렴하는 것을 방지.
- np.log1p()는 np.log(x + 1)과 동일한 역할을 함.
- 데이터의 분포가 비대칭(오른쪽으로 긴 꼬리를 가진 경우, 즉 Skewed Data)이면, 로그 변환을 적용하여 정규 분포에 가깝게 만들 수 있음.
- 선형 회귀(Linear Regression)는 정규 분포를 가정하므로 로그 변환을 통해 성능을 개선할 수 있음.
lr = LinearRegression()
lr.fit(X_train, y_train)
y_pred_log = lr.predict(X_test)
- 로그 변환된 y_train을 사용하여 선형 회귀 모델을 학습.
- lr.predict(X_test): 테스트 데이터(X_test)에 대한 로그 예측값 (y_pred_log) 생성.
#로그 예측값을 원래 값으로 변환
log_pred = np.expm1(y_pred_log)
y_test_original = np.expm1(y_test)
- 로그 변환된 값을 다시 원래 값으로 되돌리기 위해 np.expm1()을 사용.
- np.expm1(x) = exp(x) - 1, 즉 로그 변환을 했던 log1p()의 역변환.
- 변환된 결과:
- y_test_original: 원래 y_test 값(로그 변환 후 다시 복원된 값).
- log_pred: 예측값을 로그 변환 후 복원한 값.
root_mean_squared_error(y_test_original, log_pred)
- RMSE (Root Mean Squared Error, 평균 제곱근 오차) 계산:
- MSE(Mean Squared Error): 예측값과 실제값 간의 차이를 제곱 후 평균을 냄.
- RMSE: MSE에 제곱근을 취한 값으로, 값이 작을수록 모델이 더 정확함.
- 여기서 y_test_original은 실제 값이고, log_pred는 로그 변환을 거친 후 복원된 예측값.
#new_pred - log_pred
42987.37959096641 - 33187.45360971534
# 결과 : 9799.925981251072
- new_pred: 로그 변환을 적용하지 않은 모델의 예측값.
- log_pred: 로그 변환을 적용한 후 예측값을 원래 값으로 변환한 것.
- → 로그 변환을 적용한 모델이 로그 변환 전보다 예측값이 낮아졌음.
로그 변환을 적용한 이유
- 선형 회귀 모델이 이상치(outlier)와 비대칭 분포에 취약하기 때문에 로그 변환을 적용하면 더 나은 성능을 기대할 수 있음.
- 일반적으로 부동산 가격, 소득, 판매량 같은 데이터는 큰 값들이 많아 분포가 왜곡(Skewed)되는 경우가 많음.
- 로그 변환을 적용하면 데이터가 정규 분포(Normal Distribution)에 가까워지고, 모델이 더 안정적으로 학습됨.
로그 변환 전:
- 종속 변수
- y 가 매우 큰 값(아웃라이어)을 가지거나 비선형적인 분포를 가진 경우, 선형 회귀 모델이 데이터에 잘 맞지 않을 수 있습니다.
- y 값의 분포가 치우쳐 있다면, 잔차(오차)가 고르게 분포하지 않고 특정 영역에서 크게 발생할 가능성이 높습니다.
- 모델이 큰 값에 더 많은 영향을 받으므로, 과적합(overfitting) 혹은 모델의 일반화 능력 저하 가능성이 있습니다.
- 그래프 형태:
- 𝑋 - y 그래프에서 데이터 포인트들이 비선형적인 곡선을 따라 분포하거나 특정 축에 몰려있는 모습이 나타날 수 있습니다.
- 회귀선은 데이터의 흐름을 제대로 따라가지 못하고, 전체적으로 부정확한 결과를 보일 가능성이 있습니다.
관찰이나 실험으로 얻은 샘플자료(적은 수의 자료)를 분석하고 설명하기 위해서는 그 자료를 잘 표현할 수 있는 '방정식'을 예측해야 합니다. 자료를 가장 잘 설명하는 방정식이란, 원래 자료와의 오차(error)를 가장 적게 만든 식 입니다.
아래 그림의 x와 y의 분포도에 있는 저 선(Regression line)이 바로 '자료를 가장 잘 설명하는 방정식'이 됩니다.
회귀분석에서는 이 선을 '회귀선'이라고 하며, 이 회귀선의 '회귀(방정)식'을 이용하면 독립변수로 종속변수를 예측할 수 있게 됩니다.

로그 변환 후:
- 로그 변환을 통해 종속 변수 𝑦 의 분포를 더 정규화(normalize)하여 스케일을 축소합니다.
- 큰 값과 작은 값의 차이를 줄이면서 아웃라이어의 영향을 감소시킵니다.
- 𝑋 - log(y) 관계가 선형적으로 변환되기 때문에 선형 회귀 모델이 데이터에 더 잘 맞을 가능성이 높아집니다.
- 그래프 형태:
- 𝑋 - log(y) 그래프에서 데이터 포인트들이 더 직선에 가까운 형태로 정렬됩니다.
- 회귀선이 데이터의 흐름을 더 잘 따라가는 모습이 나타나며, 잔차가 고르게 분포하는 경향을 보입니다.
시각적 비교
로그 변환 전후의 그래프를 비교하면 다음과 같은 차이가 있습니다:
- 로그 변환 전:
- 데이터가 비선형 곡선을 따라 흩어져 있거나 특정 값에 몰려 있습니다.
- 회귀선이 데이터의 흐름을 잘 설명하지 못해 잔차가 커지는 경향이 있습니다.
- 로그 변환 후:
- 데이터가 선형적인 직선 형태로 정렬됩니다.
- 회귀선이 데이터의 흐름을 더 잘 설명하며, 잔차도 고르게 분포합니다.
6. 앙상블 모델 적용
앙상블 모델(Ensemble Model)은 여러 개의 머신러닝 모델을 조합하여 하나의 강력한 예측 모델을 만드는 방법입니다. 각 개별 모델(약한 학습기, Weak Learner)이 가진 장점을 결합하고 약점을 보완함으로써 예측 정확도와 안정성을 향상시킵니다. 대표적인 앙상블 기법으로는 배깅(Bagging), 부스팅(Boosting), 스태킹(Stacking)이 있으며, 랜덤 포레스트(Random Forest)와 XGBoost는 각각 배깅과 부스팅을 대표하는 알고리즘입니다. 앙상블 모델은 특히 복잡한 문제나 다양한 패턴이 존재하는 데이터셋에서 뛰어난 성능을 발휘합니다.
※ 랜덤 포레스트
랜덤 포레스트(Random Forest)는 다수의 결정 트리(Decision Tree)를 결합해 예측을 수행하는 앙상블 학습 방법입니다. 각각의 트리는 무작위로 선택된 데이터 샘플과 특성(feature)을 사용해 학습되며, 분류 문제에서는 다수결 투표, 회귀 문제에서는 평균을 통해 최종 예측값을 도출합니다. 이 방식은 과적합(overfitting) 위험을 줄이고 안정적인 성능을 보장하며, 비선형 관계를 잘 포착하고 이상치(outlier)에 강인한 특성을 가지고 있습니다. 또한, 변수 중요도(Feature Importance)를 제공해 어떤 특성이 예측에 중요한 역할을 하는지 이해할 수 있습니다.
※ XGBoost
XGBoost (eXtreme Gradient Boosting)는 그레디언트 부스팅(Gradient Boosting) 알고리즘을 기반으로 한 강력한 머신러닝 앙상블 모델입니다. 여러 개의 약한 학습기(Weak Learner), 주로 결정 트리(Decision Tree)를 순차적으로 학습시키며, 이전 트리의 오차를 보정해 예측 성능을 점진적으로 개선합니다. 정확도, 속도, 과적합 방지 측면에서 뛰어난 성능을 자랑하며, 결측치 처리, 과적합 제어, 병렬 학습 등의 기능을 지원합니다. 주로 복잡한 패턴을 학습해야 하는 대규모 데이터셋이나 비선형 데이터 문제에서 뛰어난 성능을 보입니다.
필요한 라이브러리 임포트
from sklearn.ensemble import RandomForestRegressor
from xgboost import XGBRegressor
- matplotlib.pyplot: 시각화를 위한 라이브러리 (현재 사용되지 않음).
- RandomForestRegressor: 랜덤 포레스트 회귀 모델.
- XGBRegressor: XGBoost 회귀 모델.
모델 정의
models = {
'Linear Regression' : LinearRegression(),
'Random Forest' : RandomForestRegressor(n_estimators=100, random_state=2025),
'XGBoost' : XGBRegressor(n_estimators=100, random_state=2025)
}
- 3가지 회귀 모델을 딕셔너리(models)에 저장.
- n_estimators=100: 랜덤 포레스트 및 XGBoost의 트리 개수를 100개로 설정.
- random_state=2025: 결과 재현성을 위해 랜덤 시드 설정
첫 번째 실험: 로그 변환 후 모델 학습
results = {}
for model_name, model in models.items():
model.fit(X_train, y_train)
y_pred_log = model.predict(X_test)
y_pred = np.expm1(y_pred_log) # 로그 변환된 예측값을 원래 값으로 복원
y_test_original = np.expm1(y_test) # 실제 값도 원래 값으로 복원
rmse = root_mean_squared_error(y_test_original, y_pred) # RMSE 계산
results[model_name] = rmse
print(f'{model_name} RMSE: {rmse : .2f}')
- for 문을 사용하여 각 모델을 학습 후 예측값을 얻음.
- 로그 변환된 y_train을 사용하여 학습.
- y_pred_log는 로그 변환된 값이므로, np.expm1()을 사용하여 원래 값으로 변환.
- root_mean_squared_error(y_test_original, y_pred): RMSE 계산.
- results 딕셔너리에 모델별 RMSE 저장.
최적 모델 선정
best_model = min(results, key=results.get)
print(f'Best Model: {best_model} RMSE: {results[best_model]:.2f}')

- min(results, key=results.get): RMSE가 가장 낮은 모델을 선택.
- 최적 모델 및 해당 RMSE 값을 출력.
두 번째 실험: 로그 변환 없이 모델 학습
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.3,
random_state=2025)
- 원래 데이터(X, y)를 다시 분할하여 X_train, X_test, y_train, y_test 생성.
- test_size=0.3: 데이터의 30%를 테스트 데이터로 사용.
- random_state=2025: 랜덤성을 고정하여 동일한 데이터 분할을 보장.
모델 학습 및 성능 평가 (로그 변환 없이)
results = {}
for model_name, model in models.items():
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
rmse = root_mean_squared_error(y_test, y_pred)
results[model_name] = rmse
print(f'{model_name} RMSE: {rmse : .2f}')
- for 문을 사용하여 로그 변환 없이 모델을 학습 및 예측.
- y_pred = model.predict(X_test): 예측값 생성.
- root_mean_squared_error(y_test, y_pred): 로그 변환 없이 RMSE 계산.
- results 딕셔너리에 모델별 RMSE 저장.
최적 모델 확인
best_model = min(results, key=results.get)
print(f'Best Model: {best_model} RMSE: {results[best_model]:.2f}')
로그 변환 없이 학습한 모델들 중 RMSE가 가장 낮은 모델을 선택.

'인공지능 > 데이터분석' 카테고리의 다른 글
| 파이토치로 구현한 논리 회귀 (0) | 2025.02.01 |
|---|---|
| 서울 자전거 공유 수요 예측 데이터셋 (2) | 2025.02.01 |
| 사이킷런-아이리스(Iris) 데이터셋 분석 (0) | 2025.01.31 |
| 파이토치로 구현한 선형 회귀 (0) | 2025.01.29 |
| 텐서(Tensor) (2) | 2025.01.29 |



