텐서
PyTorch의 텐서(Tensor)는 딥러닝 모델에서 데이터를 다룰 때 사용되는 기본 데이터 구조입니다. 텐서는 다차원 배열로, NumPy의 배열과 비슷하지만, GPU에서 연산을 수행할 수 있다는 점에서 차이가 있습니다. PyTorch의 텐서는 데이터의 표현뿐만 아니라, 자동 미분(autograd) 기능을 제공하여 딥러닝 모델의 학습을 도와줍니다.
1. 2D 텐서 생성
data = [
[1, 2],
[3, 4]
]
t1 = torch.tensor(data)
print(t1) # 출력: tensor([[1, 2], [3, 4]])- torch.tensor(data):
- 2D 리스트(data)를 PyTorch의 2차원 텐서로 변환.
- t1의 값:
[[1, 2], [3, 4]]
2. 텐서 연산 후 NumPy 변환
t1 = torch.tensor([5])
t2 = torch.tensor([7])
ndarr1 = (t1 + t2).numpy() # 텐서를 더하고 NumPy 배열로 변환
print(ndarr1) # 출력: [12]
print(type(ndarr1)) # 출력: <class 'numpy.ndarray'>- t1 + t2:
- 두 0차원 텐서의 값을 더한 결과는 [12].
- .numpy():
- PyTorch 텐서를 NumPy 배열로 변환.
NumPy 배열 연산 후 PyTorch 변환
result = ndarr1 * 10
t3 = torch.from_numpy(result)
print(t3) # 출력: tensor([120.], dtype=torch.float64)
print(type(t3)) # 출력: <class 'torch.Tensor'>- ndarr1 * 10:
- NumPy 배열 요소에 스칼라 곱 적용: [12 * 10] = [120].
- torch.from_numpy(result):
- NumPy 배열을 PyTorch 텐서로 변환.
3. 2D 텐서의 슬라이싱
t1 = torch.tensor([
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
])
print(t1[0]) # 첫 번째 행: tensor([1, 2, 3, 4])
print(t1[0, :]) # 첫 번째 행 전체 (행 슬라이싱): tensor([1, 2, 3, 4])
print(t1[:, 0]) # 첫 번째 열: tensor([1, 5, 9])
print(t1[:, -1]) # 마지막 열: tensor([ 4, 8, 12])
print(t1[..., -1]) # 모든 행의 마지막 열: tensor([ 4, 8, 12])슬라이싱 설명:
- t1[0]:
- 첫 번째 행(인덱스 0)을 선택.
- t1[0, :]:
- 첫 번째 행의 모든 열을 선택.
- t1[:, 0]:
- 모든 행에서 첫 번째 열만 선택.
- t1[:, -1]:
- 모든 행에서 마지막 열 선택.
- t1[..., -1]:
- **...**는 모든 차원(여기서는 행)을 선택하며, 마지막 열만 추출.
4. 3D 텐서 생성 및 슬라이싱
t1 = torch.tensor([[[1, 2, 3],
[4, 5, 6]],
[[7, 8, 9],
[10, 11, 12]]])
print(t1.shape) # 출력: torch.Size([2, 2, 3])- t1 구조:
[ [[1, 2, 3], # 첫 번째 "슬라이스" [4, 5, 6]], [[7, 8, 9], # 두 번째 "슬라이스" [10, 11, 12]] ]- 텐서의 차원:
- 첫 번째 차원: 2개의 슬라이스.
- 두 번째 차원: 각 슬라이스에 2개의 행.
- 세 번째 차원: 각 행에 3개의 열.
- 텐서의 차원:
3D 텐서 슬라이싱
print(t1[..., -1]) # 출력: tensor([[ 3, 6], [ 9, 12]])- ...:
- 앞의 모든 차원(첫 번째와 두 번째)을 선택.
- 마지막 차원(열)에서 마지막 요소만 선택:
[ [3, 6], # 첫 번째 슬라이스의 마지막 열 [9, 12] # 두 번째 슬라이스의 마지막 열 ]
정리
- 텐서 연산 및 변환:
- PyTorch 텐서 ↔ NumPy 배열 간 변환은 .numpy()와 torch.from_numpy()로 가능.
- NumPy 배열로 변환 후 연산을 수행하고 다시 텐서로 변환할 수 있음.
- 슬라이싱:
- :: 특정 차원의 모든 요소 선택.
- ...: 모든 앞 차원을 유지하며 특정 차원의 요소를 선택.
- 3D 텐서 활용:
- 고차원 텐서는 이미지, 시계열 데이터 등에서 자주 사용.
- ... 연산자를 사용하면 다양한 차원에서 편리하게 요소를 선택 가능.
GPU 사용
GPU (Graphics Processing Unit)는 그래픽 처리 장치로, 주로 이미지 렌더링과 같은 대규모 병렬 계산을 수행하는 데 최적화된 하드웨어입니다. 원래는 그래픽 처리를 위해 설계되었지만, 최근에는 인공지능(AI) 및 딥러닝의 연산 가속기로 널리 사용되고 있습니다. 딥러닝은 수천, 수만 개의 행렬 및 벡터 연산을 필요로 합니다. GPU는 여러 개의 코어를 사용하여 이 연산을 병렬로 처리할 수 있습니다. 따라서 GPU는 딥러닝 에 최적화된 구조를 가지고 있습니다.
1. 텐서 생성
data = [
[1, 2],
[3, 4]
]
t1 = torch.tensor(data)
print(t1)
print(t1.is_cuda) # 출력: False- torch.tensor(data):
- 2D 리스트를 CPU 텐서로 생성합니다. 기본적으로 텐서는 CPU에 저장됩니다.
- t1.is_cuda:
- 텐서가 GPU에 저장되어 있는지 확인하는 속성.
- 출력값이 False인 이유:
- t1은 기본적으로 CPU에서 생성되었기 때문입니다.
2. 텐서를 GPU로 옮기기
t1 = t1.cuda() # GPU로 옮김
print(t1.is_cuda) # 출력: True- t1.cuda():
- t1 텐서를 GPU 메모리로 전송합니다.
- GPU에서의 연산은 CPU보다 병렬 처리가 가능해 속도가 빠릅니다.
- t1.is_cuda:
- GPU에 저장되었는지 확인하며, 이제 True를 반환합니다.
3. 텐서를 다시 CPU로 옮기기
t1 = t1.cpu() # CPU로 옮김
print(t1.is_cuda) # 출력: False- t1.cpu():
- GPU에 저장된 텐서를 다시 CPU로 전송합니다.
- t1.is_cuda:
- 텐서가 GPU에 있지 않음을 확인하며, 다시 False로 반환됩니다.
4. CPU와 GPU 텐서 연산
t1 = torch.tensor([
[1, 1],
[2, 2]
]).cuda()
t2 = torch.tensor([
[5, 6],
[7, 8]
])- t1:
- GPU에 저장된 텐서.
- t2:
- CPU에 저장된 텐서.
GPU와 CPU 텐서 연산
# print(torch.matmul(t1, t2)) # 오류 발생- 오류 이유:
- t1은 GPU에, t2는 CPU에 있으므로 두 텐서 간 연산이 불가능합니다.
- PyTorch에서는 CPU와 GPU 간 텐서를 직접 연산할 수 없으며, 동일한 디바이스에서만 연산이 가능합니다.
해결 방법
print(torch.matmul(t1.cpu(), t2)) # 출력: tensor([[12, 14], [24, 28]])- t1.cpu():
- t1을 GPU에서 CPU로 옮긴 후 t2와 연산.
- torch.matmul:
- 두 텐서의 행렬 곱(Matrix Multiplication)을 수행.
- 계산 과정:
[[1*5 + 1*7, 1*6 + 1*8], => [[12, 14], [2*5 + 2*7, 2*6 + 2*8]] [24, 28]]
5. 텐서의 디바이스 확인
print(f"Device: {t1.device}") # 출력: cpu- t1.device:
- 텐서가 현재 저장된 디바이스(CPU 또는 GPU)를 반환.
- t1.cpu()로 이동했으므로 디바이스는 cpu로 표시됩니다.
정리
- 디바이스 속성 확인:
- is_cuda: 텐서가 GPU에 저장되어 있는지 확인.
- device: 텐서가 저장된 디바이스를 반환.
- CPU ↔ GPU 전송:
- cuda(): 텐서를 GPU로 전송.
- cpu(): 텐서를 CPU로 전송.
- GPU와 CPU 텐서 연산:
- 동일한 디바이스에 있는 텐서끼리만 연산 가능.
- CPU와 GPU 간 연산을 위해 한쪽을 다른 쪽으로 전송해야 함.
- 행렬 곱:
- torch.matmul: 두 텐서 간 행렬 곱을 수행.
텐서의 연산과 함수
1. 기본 연산
t1 = torch.tensor([
[1, 2],
[3, 4]
])
t2 = torch.tensor([
[5, 6],
[7, 8]
])
print(t1 + t2) # 요소별 덧셈
print(t1 - t2) # 요소별 뺄셈
print(t1 * t2) # 요소별 곱셈
print(t1 / t2) # 요소별 나눗셈요소별 연산 (Element-wise Operations):
- t1 + t2:
- 각 요소를 동일한 위치에서 더합니다.
- 결과:
[[1+5, 2+6], [3+7, 4+8]] = [[6, 8], [10, 12]]
- t1 - t2:
- 각 요소를 동일한 위치에서 뺍니다.
- 결과:
[[1-5, 2-6], [3-7, 4-8]] = [[-4, -4], [-4, -4]]
- t1 * t2:
- 각 요소를 동일한 위치에서 곱합니다.
- 결과:
[[1*5, 2*6], [3*7, 4*8]] = [[5, 12], [21, 32]]
- t1 / t2:
- 각 요소를 동일한 위치에서 나눕니다.
- 결과:
[[1/5, 2/6], [3/7, 4/8]] = [[0.2, 0.3333], [0.4286, 0.5]]
2. 행렬 곱
print(t1.matmul(t2)) # 또는 torch.matmul(t1, t2)- 행렬 곱 (Matrix Multiplication):
- torch.matmul 또는 t1.matmul(t2)은 행렬 곱을 수행합니다.
- 계산 과정:
[[(1*5 + 2*7), (1*6 + 2*8)], [(3*5 + 4*7), (3*6 + 4*8)]] = [[19, 22], [43, 50]]
3. 평균 계산
t1 = torch.Tensor([
[1, 2, 3, 4],
[5, 6, 7, 8]
])
print(t1.mean()) # 전체 원소 평균
print(t1.mean(dim=0)) # 각 열 평균
print(t1.mean(dim=1)) # 각 행 평균평균 계산:
- t1.mean():
- 전체 원소에 대한 평균:
(1+2+3+4+5+6+7+8) / 8 = 4.5
- 전체 원소에 대한 평균:
- t1.mean(dim=0):
- 각 열에 대해 평균 계산:
[ (1+5)/2, (2+6)/2, (3+7)/2, (4+8)/2 ] = [3.0, 4.0, 5.0, 6.0]
- 각 열에 대해 평균 계산:
- t1.mean(dim=1):
- 각 행에 대해 평균 계산:
[ (1+2+3+4)/4, (5+6+7+8)/4 ] = [2.5, 6.5]
- 각 행에 대해 평균 계산:
4. 합계 계산
print(t1.sum()) # 전체 원소 합계
print(t1.sum(dim=0)) # 각 열 합계
print(t1.sum(dim=1)) # 각 행 합계합계 계산:
- t1.sum():
- 전체 원소에 대한 합계 계산:
1+2+3+4+5+6+7+8 = 36
- t1.sum(dim=0):
- 각 열에 대해 합계 계산:
[ 1+5, 2+6, 3+7, 4+8 ] = [6, 8, 10, 12]
- 각 열에 대해 합계 계산:
- t1.sum(dim=1):
- 각 행에 대해 합계 계산:
[ 1+2+3+4, 5+6+7+8 ] = [10, 26]
- 각 행에 대해 합계 계산:
5. 최댓값 인덱스 계산
print(t1.argmax()) # 전체 원소 중 최댓값의 인덱스
print(t1.argmax(dim=0)) # 각 열에서 최댓값의 인덱스
print(t1.argmax(dim=1)) # 각 행에서 최댓값의 인덱스최댓값 인덱스 계산:
- t1.argmax():
- 텐서를 1D로 펼쳐 최댓값의 플랫(flat) 인덱스를 반환:
원소: [1, 2, 3, 4, 5, 6, 7, 8] 최댓값 8의 인덱스: 7
- 텐서를 1D로 펼쳐 최댓값의 플랫(flat) 인덱스를 반환:
- t1.argmax(dim=0):
- 각 열에서 최댓값의 인덱스를 반환:
열별로 [max(1,5), max(2,6), max(3,7), max(4,8)] 인덱스: [1, 1, 1, 1]
- 각 열에서 최댓값의 인덱스를 반환:
- t1.argmax(dim=1):
- 각 행에서 최댓값의 인덱스를 반환:
행별로 [max(1,2,3,4), max(5,6,7,8)] 인덱스: [3, 3]
- 각 행에서 최댓값의 인덱스를 반환:
정리
- 기본 연산:
- 요소별 덧셈, 뺄셈, 곱셈, 나눗셈은 동일 위치의 값을 연산.
- 행렬 곱:
- torch.matmul 또는 .matmul을 사용.
- 평균, 합계:
- dim을 지정하지 않으면 전체 원소 기준으로 계산.
- dim=0: 각 열 기준.
- dim=1: 각 행 기준.
- 최댓값 인덱스:
- argmax()는 전체 또는 지정한 차원의 최댓값 인덱스를 반환.
텐서의 차원 조작
1. 텐서 이어 붙이기 (torch.cat)
1-1. 0번 축(행)을 기준으로 이어 붙이기
result = torch.cat([t1, t1, t1], dim=0)
print(result)- dim=0: 행 기준으로 텐서를 이어 붙입니다.
- 결과:
- 원래 t1은 [3x4] 형태입니다.
- 행 방향으로 3개를 이어 붙이면 [9x4] 크기의 텐서가 됩니다.
1-2. 1번 축(열)을 기준으로 이어 붙이기
result = torch.cat([t1, t1, t1], dim=1)
print(result)- dim=1: 열 기준으로 텐서를 이어 붙입니다.
- 결과:
- 원래 t1은 [3x4] 형태입니다.
- 열 방향으로 3개를 이어 붙이면 [3x12] 크기의 텐서가 됩니다.
2. 텐서의 데이터 타입
데이터 타입 확인 및 변환
t1 = torch.tensor([2], dtype=torch.int)
t2 = torch.tensor([5.0])
print(t1.dtype) # 출력: torch.int32 (또는 시스템에 따라 int64)
print(t2.dtype) # 출력: torch.float32- 텐서의 데이터 타입(dtype)은 연산에 영향을 미칩니다.
자동 형 변환
print(t1 + t2) # 출력: tensor([7.], dtype=torch.float32)- PyTorch는 형 변환 우선순위에 따라 t1이 float32로 변환되어 연산을 수행합니다.
명시적 형 변환
print(t1 + t2.type(torch.int32)) # 출력: tensor([7], dtype=torch.int32)- t2.type(torch.int32):
- t2를 int32로 변환하여 연산을 수행합니다.
- 결과는 int32가 됩니다.
3. 텐서 모양 변경 (view)
3-1. view를 사용한 모양 변경
t1 = torch.tensor([1, 2, 3, 4, 5, 6, 7, 8])
t2 = t1.view(4, 2)
print(t2)- view(4, 2):
- t1을 [4x2] 모양으로 변환합니다.
- view는 원본 데이터를 참조하므로 메모리를 공유합니다.
3-2. 원본 데이터 변경 시 영향
t1[0] = 7
print(t1) # t1의 첫 번째 값이 변경됨
print(t2) # t2에서도 첫 번째 값이 변경됨- t1과 t2는 데이터를 공유하므로, 하나를 변경하면 다른 하나에도 반영됩니다.
3-3. clone을 사용한 데이터 복사
t3 = t1.clone().view(4, 2)
t1[0] = 9
print(t1) # t1이 변경됨
print(t3) # t3는 영향을 받지 않음- clone():
- t1의 복사본을 생성합니다.
- 복사된 텐서는 독립된 메모리를 사용하므로 변경이 서로 영향을 미치지 않습니다.
4. 텐서 차원 조작
4-1. 차원 교환 (permute)
t1 = torch.rand((64, 32, 3))
t2 = t1.permute(2, 1, 0)
print(t2.shape) # 출력: torch.Size([3, 32, 64])- permute:
- 텐서의 차원을 재배치합니다.
- (2, 1, 0)은 기존의 [64, 32, 3] 차원을 [3, 32, 64]로 교환합니다.
4-2. 차원 추가 (unsqueeze)
t1 = t1.unsqueeze(0)
print(t1.shape) # 출력: torch.Size([1, 64, 32, 3])- unsqueeze(dim=0):
- 0번 축(가장 바깥쪽)에 크기가 1인 차원을 추가합니다.
- 결과: [1x64x32x3].
4-3. 차원 제거 (squeeze)
t1 = t1.unsqueeze(3) # 차원 추가
print(t1.shape) # 출력: torch.Size([1, 64, 32, 3, 1])
t1 = t1.squeeze()
print(t1.shape) # 출력: torch.Size([64, 32, 3])- squeeze():
- 크기가 1인 차원을 제거합니다.
- 특정 차원을 지정하면, 해당 차원이 1인 경우에만 제거됩니다.
정리
- 텐서 결합:
- torch.cat으로 여러 텐서를 지정된 축(dim)을 기준으로 결합 가능.
- 데이터 타입 관리:
- PyTorch는 형 변환 우선순위에 따라 자동으로 변환하지만, type()으로 명시적 변환이 가능.
- 텐서 모양 변경:
- view: 텐서의 모양을 변경하며 원본 데이터를 참조.
- clone: 독립적인 복사본 생성.
- 차원 조작:
- permute: 차원 순서를 변경.
- unsqueeze: 차원을 추가.
- squeeze: 크기가 1인 차원을 제거.
자동 미분과 기울기
PyTorch의 자동 미분(Autograd) 기능을 활용하여 텐서의 연산을 기록하고, 역전파(Backpropagation)를 통해 기울기(gradient)를 계산하는 과정을 공부해보자
1. requires_grad=True의 의미
x = torch.tensor([3.0, 4.0], requires_grad=True)
y = torch.tensor([1.0, 2.0], requires_grad=True)- requires_grad=True:
- 텐서가 연산에 사용되며, 해당 연산의 결과에 대해 기울기(gradient)를 계산하겠다는 의미입니다.
- PyTorch는 이 텐서가 사용된 모든 연산을 연산 그래프(Computational Graph)에 기록합니다.
- 이후 역전파를 통해 각 텐서의 기울기를 자동으로 계산합니다.
2. 연산 과정
z = x + y
print(z) # 출력: tensor([4., 6.], grad_fn=<AddBackward0>)- z = x + y:
- 텐서 x와 y의 요소별 덧셈.
- 결과 텐서 z는 연산 그래프에 연결되며, grad_fn 속성을 가집니다.
- grad_fn=<AddBackward0>:
- 이 텐서는 x와 y를 더한 연산에서 파생되었음을 나타냅니다.
- 역전파 시 이 연산의 기울기를 계산합니다.
out = z.mean()
print(out) # 출력: tensor(5., grad_fn=<MeanBackward0>)- z.mean():
- 텐서 z의 모든 요소의 평균을 계산.
- 결과 텐서 out은 연산 그래프의 또 다른 노드가 됩니다.
3. 역전파 (backward)
out.backward() # 역전파 시작- backward():
- out으로부터 시작하여 연산 그래프를 거슬러 올라가며, 각 텐서에 대한 기울기를 계산합니다.
- 역전파의 목표는 최종 스칼라 값(out)이 각 입력 텐서(x, y)에 대해 얼마나 빠르게 변화하는지를 측정하는 것입니다.
- 이를 기울기(gradient)라고 하며, 계산 결과는 각 텐서의 .grad 속성에 저장됩니다.
4. 기울기 확인
print("x.grad:", x.grad)
print("y.grad:", y.grad)
print("z.grad:", z.grad) # 출력: None
(1) x.grad와 y.grad
- out에 대한 x와 y의 기울기는 다음과 같이 계산됩니다:
수식:

각각의 요소별 미분:

결과:

(2) z.grad
- z.grad는 None으로 출력됩니다.
- 이유:
- z는 중간 연산 결과로, backward()가 호출되었을 때 직접적으로 기울기를 요구하지 않았습니다.
- 중간 노드의 기울기를 확인하려면 retain_graph=True 옵션이 필요합니다.
5. 역전파(Backpropagation)의 원리
역전파는 연산 그래프에서 연쇄 법칙(Chain Rule)을 사용하여 기울기를 계산하는 알고리즘입니다.
연쇄 법칙 (Chain Rule)
- 함수 f 와 g 가 있을 때, 합성 함수 h(x)= g(f(x)) 의 도함수는: h′(x)=g′(f(x))⋅f′(x)
적용
- 그래프 생성:
- PyTorch는 텐서의 연산을 기록하여 그래프를 생성합니다.
- 예: z=x+y, out=mean(z)out = mean
- 기울기 계산:
- 역전파는 출력에서 입력 방향으로 그래프를 따라가며, 연쇄 법칙을 이용해 각 텐서의 기울기를 계산합니다.
- 예

7. 역전파의 실제 활용
- 기울기 계산은 최적화 문제에서 매우 중요합니다.
- 딥러닝에서 손실 함수(Loss Function)에 대한 가중치(Weights)의 기울기를 계산하여, 경사 하강법(Gradient Descent)으로 가중치를 갱신합니다.
- 예:
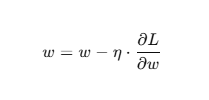
- 여기서:
- w: 가중치
- L: 손실 함수
- η: 학습률(Learning Rate)
'인공지능 > 데이터분석' 카테고리의 다른 글
| 판다스-기초1 (0) | 2025.01.16 |
|---|---|
| 넘파이 - 기초 (0) | 2025.01.16 |
| 파이토치 프레임워크 (0) | 2025.01.06 |
| 머신러닝 (2) | 2025.01.06 |
| 인공지능과 머신러닝, 딥러닝 (0) | 2025.01.06 |



