서울 자전거 공유 수요 데이터셋
서울시의 공공자전거 대여 서비스인 ‘따릉이’의 대여 수요를 예측하는 문제에 사용되는 데이터셋입니다. 특정 시간대와 날씨, 요일, 공휴일 여부, 기온, 습도 등 다양한 데이터를 활용하여 자전거 대여 수요를 예측합니다.
https://www.kaggle.com/datasets/joebeachcapital/seoul-bike-sharing/data
Seoul Bike Sharing Demand Prediction
Predict demand for shared bikes in Seoul based on various environmental factors
www.kaggle.com
데이터셋 컬럼
- Date : 연월일
- Rented Bike count - 매 시간마다 대여한 자전거 수
- Hour - 하루 중 시간
- Temperature - 온도
- Humidity - 습도 %
- Windspeed - 풍속 m/s
- Visibility - 가시거리 m
- Dew point temperature - 이슬점 온도
- Solar radiation - 태양 복사 MJ/m2
- Rainfall - 강우량 mm
- Snowfall - 적설량 cm
- Seasons - 겨울, 봄, 여름, 가을
- Holiday - 휴일/휴일 없음
- Functional Day - 운영되지 않았던 날, 정상적으로 운영된 날
데이터 전처리 및 탐색적 데이터 분석 (EDA)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns# CP949
# Microsoft Windows의 한국어 문자 인코딩입니다.
# EUC-KR을 확장한 형태로, 더 많은 한국어 문자(한자, 확장 문자 등)를 지원합니다.
# 주로 Windows 환경에서 저장된 한글 파일에서 사용됩니다.
bike_df = pd.read_csv('/내드라이브 경로/SeoulBikeData.csv',encoding='CP949')
bike_df
bike_df.info()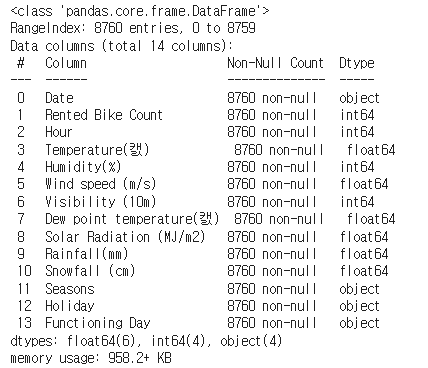
bike_df.describe()
bike_df.columns
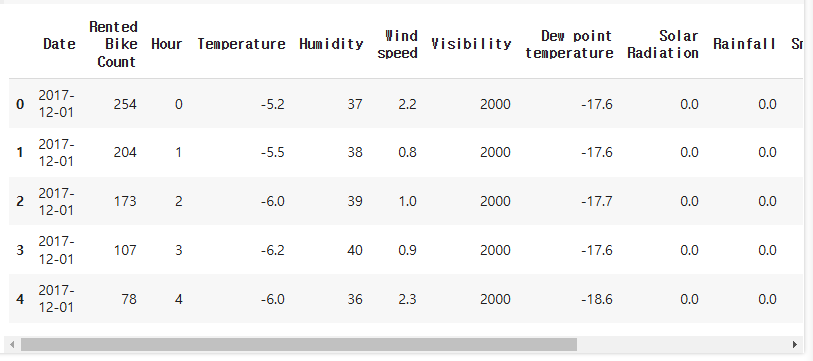
bike_df.columns = ['Date', 'Rented Bike Count', 'Hour', 'Temperature', 'Humidity',
'Wind speed', 'Visibility', 'Dew point temperature',
'Solar Radiation', 'Rainfall', 'Snowfall', 'Seasons',
'Holiday', 'Functioning Day']bike_df.head()
scatterplot
산점도 (Scatter plot)는 두 변수의 상관 관계를 직교 좌표계의 평면에 점으로 표현하는 그래프입니다.
matplotlib.pyplot 모듈의 scatter() 함수를 이용하면 산점도를 그릴 수 있습니다.
sns.scatterplot(data=bike_df, x='Temperature', y='Rented Bike Count',alpha=0.3)1. Temperature (온도) vs. Rented Bike Count (대여량)
📌 해석:
- 온도가 높아질수록 자전거 대여량이 증가하는 양의 상관관계(Positive Correlation)를 보임.
- 특히 0도 이하에서는 대여량이 적고, 10~30도 사이에서 대여량이 많아지는 경향을 보임.
- 그러나 30도 이상에서는 증가세가 둔화되거나 약간 감소하는 경향도 보일 수 있음.
📢 인사이트:
- 날씨가 따뜻할수록 사람들이 자전거를 더 많이 이용한다.
- 하지만 너무 더운 날(30도 이상)에는 이용량이 정체되거나 줄어들 수 있음.

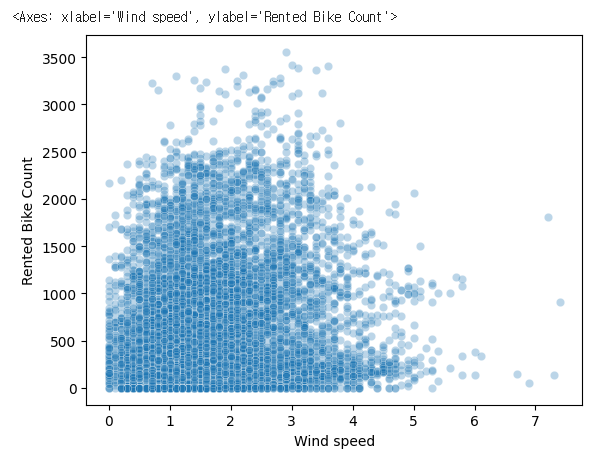
sns.scatterplot(data=bike_df, x='Wind speed', y='Rented Bike Count',alpha=0.3)2. Wind Speed (풍속) vs. Rented Bike Count (대여량)
📌 해석:
- 풍속(Wind Speed)과 자전거 대여량 사이에 뚜렷한 패턴이 보이지 않음.
- 대부분의 데이터가 풍속 0~4 m/s 범위에서 분포.
- 풍속이 높아질수록 약간의 감소 경향이 보이긴 하지만 명확한 패턴은 없음.
📢 인사이트:
- 풍속이 자전거 대여에 미치는 영향은 크지 않음.
- 다만, 강한 바람(5m/s 이상)에서는 자전거 대여량이 줄어들 가능성이 있음.
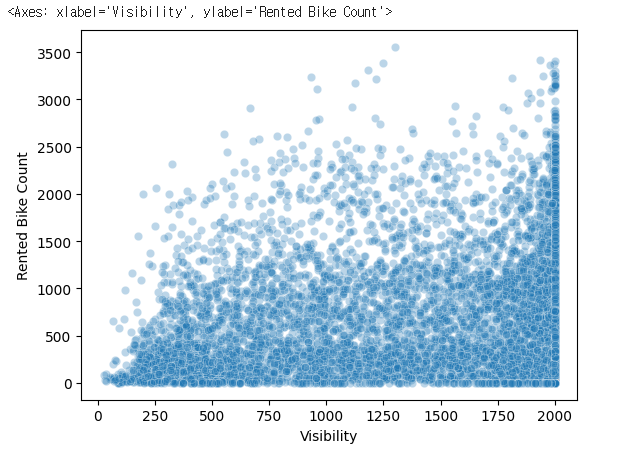
sns.scatterplot(data=bike_df, x='Visibility', y='Rented Bike Count',alpha=0.3)3. Visibility (가시거리) vs. Rented Bike Count (대여량)
📌 해석:
- 가시거리가 높을수록(=날씨가 맑을수록) 자전거 대여량이 많아지는 경향.
- 하지만 가시거리가 낮아도(안개가 많거나 미세먼지가 많은 경우) 자전거 대여량이 아주 낮지는 않음.
- 전반적으로 가시거리와 자전거 대여량 간의 직접적인 상관관계는 크지 않음.
📢 인사이트:
- 맑은 날씨(가시거리가 좋은 날)에 자전거 대여량이 많아질 가능성이 있음.
- 하지만 가시거리가 낮아도 사람들이 자전거를 많이 이용하는 경우가 존재.
sns.scatterplot(data=bike_df, x='Hour', y='Rented Bike Count',alpha=0.3)4. Hour (시간) vs. Rented Bike Count (대여량)
📌 해석:
- 자전거 대여량이 특정 시간대에서 뚜렷하게 증가하는 패턴이 보임.
- 출근 시간(8
9시)과 퇴근 시간(1719시)에서 자전거 이용량이 급증. - 새벽 시간(0~5시)에는 대여량이 적음.
- 점심시간(12~13시)에도 대여량이 약간 증가하는 경향.
📢 인사이트:
- 자전거 대여는 출퇴근 시간대에 가장 활발.
- 새벽 시간에는 거의 사용되지 않음.
- 대중교통과의 연계 수요가 클 가능성.

결측지 확인
bike_df.isna().sum()
날짜는 date형식으로 변환
bike_df['Date'] = pd.to_datetime(bike_df['Date'],format='%d/%m/%Y')
bike_df.info()
bike_df.head()
date를 각각 년,월,일로 나누기
bike_df['year'] = bike_df['Date'].dt.year
bike_df['month'] = bike_df['Date'].dt.month
bike_df['day'] = bike_df['Date'].dt.day
bike_df.head()
lineplot
선 그래프 시간에 따라 변화하는 모양을 나타내는 데 편리
plt.figure(figsize=(14,4))
sns.lineplot(x='Date', y='Rented Bike Count', data=bike_df)
plt.xticks(rotation=45)
plt.show()
2017년도는 무슨 몇월이 데이터셋에 포함되었는지 월별로 확인
bike_df[bike_df['year'] == 2017].groupby('month')['Rented Bike Count'].mean()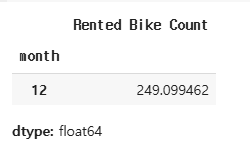
2018년도는 무슨 몇월이 데이터셋에 포함되었는지 월별로 확인
bike_df[bike_df['year'] == 2018].groupby('month')['Rented Bike Count'].mean()

시간이 너무 나누어져있기에 범주형 데이터로 변환
bike_df['TimeOfDay']= pd.cut(bike_df['Hour'], bins=[0,5,11,17,23], labels=['Dawn', 'Morning', 'Afternoon', 'Evening'], include_lowest=True)
bike_df.head()시간(Hour) 데이터를 4개의 그룹으로 나눔:
- 0 ~ 5시 → 'Dawn' (새벽)
- 5 ~ 11시 → 'Morning' (아침)
- 11 ~ 17시 → 'Afternoon' (오후)
- 17 ~ 23시 → 'Evening' (저녁)

※ pd.cut()
- pd.cut()은 숫자 데이터를 구간(bins)으로 나누어 범주형 데이터로 변환하는 데 사용됩니다. 주로 연속형 데이터를 특정 범주로 분류할 때 활용됩니다.
- bins: 숫자 데이터를 나눌 경계값(구간)입니다.
- 0 ≤ Hour ≤ 5 Dawn (새벽)
- 5 < Hour ≤ 11 Morning (아침)
- 11 < Hour ≤ 17 Afternoon (오후)
- 17 < Hour ≤ 23 Evening (저녁)
- 주의: bins의 경계값은 오른쪽 경계값을 포함합니다.
barplot
바 그래프 : 다중 클래스의 데이터가 클래스 별로 골고루 분포되어 있는지 확인할 때 유용합니다.
sns.barplot(x='Functioning Day', y='Rented Bike Count', data=bike_df)
Functioning Day 값 확인
bike_df['Functioning Day'].value_counts()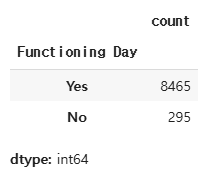
bike_df[bike_df['Functioning Day'] == 'Yes']
bike_df[bike_df['Functioning Day'] == 'No']
아까 date는 년 월 일로 나눴기에 date삭제
bike_df = bike_df.drop(['Date'], axis=1)
bike_df.head()bike_df.info()
숫자형 데이터가 아닌 콜럼 출력
bike_df.select_dtypes(exclude=['number']).columns.tolist()
# ['Seasons', 'Holiday', 'Functioning Day', 'TimeOfDay']
for i in bike_df.select_dtypes(exclude=['number']).columns.tolist():
print(i,bike_df[i].nunique())
#Seasons 4
#Holiday 2
#Functioning Day 2
#TimeOfDay 4데이터프레임(bike_df)에서 범주형 변수(숫자가 아닌 데이터)만 선택하여 각 열의 고유한 값 개수(nunique())를 출력
bike_df = pd.get_dummies(bike_df, columns=bike_df.select_dtypes(exclude=['number']).columns.tolist(),drop_first=True)
bike_df.head()
- 범주형 변수를 원-핫 인코딩(One-Hot Encoding)으로 변환하여 머신러닝 모델에서 사용할 수 있도록 숫자형 데이터로 변환.
- drop_first=True 옵션을 사용하여 더미 변수 함정을 방지.
코드 상세 설명
- bike_df.select_dtypes(exclude=['number']).columns.tolist()
→ 범주형 데이터 컬럼들을 리스트로 가져옴. - pd.get_dummies(bike_df, columns=[범주형 컬럼 리스트])
→ 해당 컬럼들을 원-핫 인코딩(One-Hot Encoding) 적용. - drop_first=True
→ 첫 번째 범주를 삭제하여 더미 변수 함수를 방지 (예: n개의 범주가 있을 때 n-1개의 컬럼만 생성).
# 모든 컬럼 간 상관관계 분석
correlation_matrix = bike_df.corr()
correlation_matrix
target_corr = correlation_matrix['Rented Bike Count'].sort_values(ascending=False)
target_corr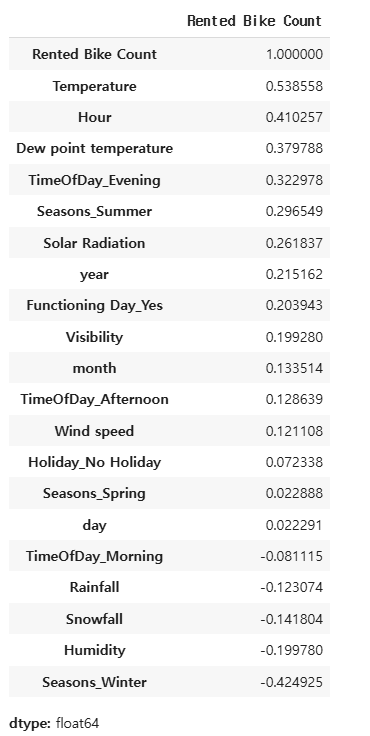
※ corr() 함수
- corr() 함수는 데이터프레임의 숫자형 열 간의 상관관계를 계산하는 데 사용됩니다. 상관관계는 두 변수 간의 선형 관계를 나타내며, 주로 -1에서 1 사이의 값으로 표현됩니다.
- corr()는 Pearson 상관계수를 기본으로 사용합니다.
- 숫자형 열만 상관관계 분석에 포함됩니다.
- 높은 상관관계(>|0.5|): 강한 관계
- 낮은 상관관계(<|0.2|): 약한 관계
- corr()를 사용하여 높은 상관관계를 가진 컬럼을 식별하고 제거할지 여부를 판단할 수 있습니다. 특히, 다중공선성(multicollinearity) 문제가 발생할 경우 머신러닝 모델의 성능이 저하될 수 있으므로, 상관관계가 높은 컬럼을 적절히 제거하는 것이 중요합니다.
※ 다중공선성
- 다중공선성(Multicollinearity)은 회귀 분석에서 독립 변수들(설명 변수) 간에 강한 상관관계가 존재하는 현상을 의미합니다. 이러한 상관관계가 높으면 각 독립 변수가 종속 변수에 미치는 개별적인 영향을 정확하게 추정하기 어려워지며, 회귀 계수의 추정치가 불안정해져 작은 데이터 변화에도 크게 변할 수 있습니다. 이는 모델의 예측 성능 저하와 해석의 신뢰성 감소로 이어질 수 있으므로, 다중공선성이 높은 변수를 식별하고 제거하거나 조정하는 것이 중요합니다.
heat map
히트맵 (heat map) : 열분포도
2차원 수치 데이터를 색으로 표시
히트맵은 각 변수 간의 상관관계(Correlation)를 시각적으로 보여주는 그래프입니다. 이를 분석하여 불필요한 변수를 제거합니다
plt.figure(figsize=(16, 12))
sns.heatmap(correlation_matrix, annot=True, fmt='.2f', cmap='coolwarm')
plt.title('Feature Correlation Heatmap')
plt.show()히트맵 해석 방법
- 색상 의미:
- 붉은색(빨간색 → 진한 빨강): 양의 상관관계(Positive Correlation) (1에 가까울수록 강한 양의 관계)
- 파란색(파랑 → 진한 파랑): 음의 상관관계(Negative Correlation) (-1에 가까울수록 강한 음의 관계)
- 흰색(0에 가까운 값): 거의 상관관계가 없음
- 대각선(1.00):
- 같은 변수끼리는 당연히 상관관계가 1이므로, 대각선은 항상 1.00.
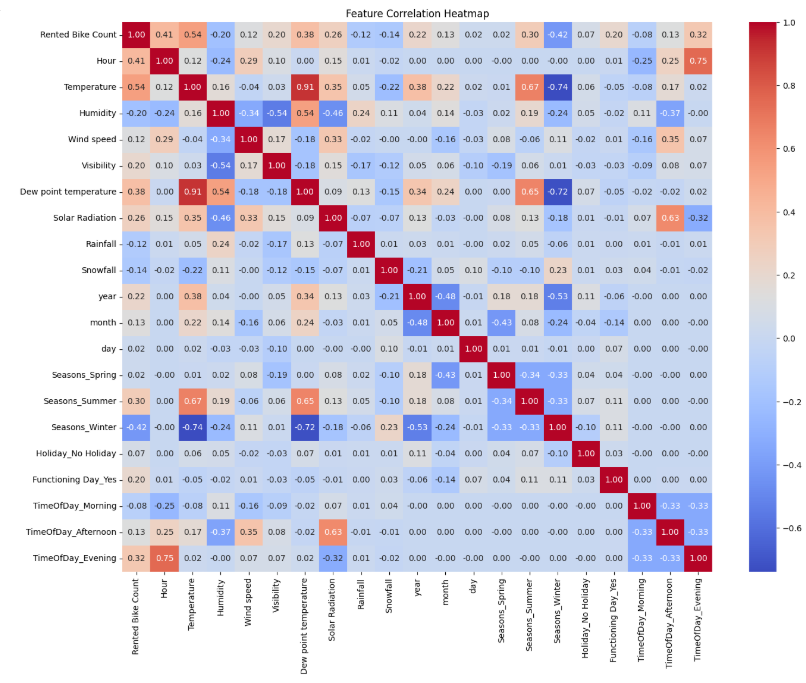
이 히트맵의 각각의 값들은 상관계수(Correlation Coefficient) 를 계산한 결과입니다.
각 변수 간의 피어슨 상관계수(Pearson Correlation Coefficient) 를 계산하여 나온 값입니다.
1. 상관계수(Pearson Correlation Coefficient)란?
두 변수 간의 선형 관계(linear relationship)를 나타내는 값으로, -1 ~ 1 사이의 값을 가짐.

2. 계산 과정 예제
예제: Temperature (기온)과 Rented Bike Count (자전거 대여량)의 상관계수 계산


히트맵 분석을 토대로 상관관계가 적은 데이터 열 삭제
bike_df = bike_df.drop(['Dew point temperature', 'Visibility','day'], axis=1)
bike_df.head()
학습 데이터와 테스트 데이터 나누기
from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(bike_df.drop('Rented Bike Count', axis=1),
bike_df['Rented Bike Count'],
test_size=0.3,
random_state=2025)X_train.shape, X_test.shape
# ((6132, 17), (2628, 17))y_train.shape, y_test.shape
# ((6132,), (2628,))4. 결정 트리
결정 트리(Decision Tree)는 데이터를 기반으로 의사결정을 수행하는 트리 구조의 예측 모델입니다. 루트 노드(root node)에서 시작해 각 노드는 특정 특성(feature)의 조건에 따라 가지(branch)로 분기되며, 최종적으로 리프 노드(leaf node)에 도달해 예측 결과(클래스나 값)를 도출합니다. 주로 분류(Classification)와 회귀(Regression) 문제에 사용되며, 데이터의 패턴을 직관적으로 시각화할 수 있어 해석이 용이합니다. 하지만 트리가 너무 깊어지면 과적합(overfitting) 문제가 발생할 수 있으므로 가지치기(pruning)나 최대 깊이 설정 등으로 제어해야 합니다.
학습 과정
- 전체 데이터셋을 하나의 노드로 시작합니다.
- 최적의 특성(feature)과 분할 기준(threshold)을 찾아 첫 번째 분할을 수행합니다.
- 분류 (Classification):
- Gini 불순도(Gini Impurity)
- 엔트로피(Entropy)
- 회귀 (Regression):
- 평균 제곱 오차(Mean Squared Error, MSE)
- 절대 평균 오차(Mean Absolute Error, MAE)
- 분류 (Classification):
- 각 하위 노드에 대해 위 단계를 반복합니다.
- 이 과정을 통해 트리는 여러 깊이로 성장합니다.
- 모든 노드가 더 이상 나눌 수 없거나 특정 조건(max_depth, min_samples_split)을 * 만족할 때까지 반복됩니다.
- 더 이상 분할이 불가능할 때 리프 노드가 생성됩니다.
- 분류 문제: 가장 많은 클래스가 있는 클래스를 예측값으로 사용
- 회귀 문제: 평균값을 예측값으로 사용
※ Gini 불순도 (Gini Impurity)
Gini 불순도는 한 노드에 있는 데이터의 순수도(Purity)를 측정하는 지표입니다. 한 노드에 있는 샘플들이 동일한 클래스에 속할 확률이 높을수록 Gini 불순도는 낮아집니다. 즉, 노드가 "얼마나 섞여 있는지"를 나타냅니다.
※ 엔트로피 (Entropy)
엔트로피는 정보의 불확실성(혼란도, Uncertainty)을 측정합니다. 엔트로피가 높을수록 해당 노드에 있는 데이터는 더 섞여 있으며, 예측하기 어렵습니다. 엔트로피는 데이터가 균등하게 분포될 때 최대값을 가집니다.
머신러닝 회귀 모델 비교 및 피처 중요도 분석
결정 트리(Decision Tree), 랜덤 포레스트(Random Forest), 선형 회귀(Linear Regression) 등의 모델을 활용하여 자전거 대여량 예측을 수행하고, 모델 성능 비교 및 중요 변수 분석을 진행해보겠습니다.
from sklearn.tree import DecisionTreeRegressordtr = DecisionTreeRegressor(random_state=2025)
dtr.fit(X_train, y_train)
pred1 = dtr.predict(X_test)
sns.scatterplot(x=y_test, y=pred1)
#같은 값으로 증가하면 예측을 어느정도 잘하고 있다고 볼 수 있다
- DecisionTreeRegressor()를 사용하여 회귀 모델을 생성하고 학습.
- predict(X_test)를 사용해 테스트 데이터에 대한 예측값(pred1)을 생성.
- sns.scatterplot(x=y_test, y=pred1)을 통해 실제값(y_test)과 예측값(pred1)의 분포를 시각화.
- 점들이 대각선에 가까울수록 예측이 잘 된 것.

모델 성능 평가 (RMSE 계산)
from sklearn.metrics import root_mean_squared_errorroot_mean_squared_error(y_test, pred1)
# 314.3922587940898RMSE 값이 낮을수록 모델 성능이 좋음.
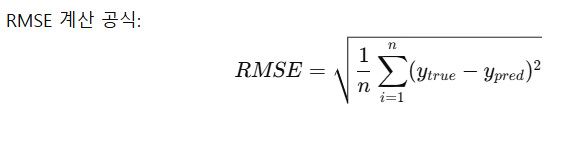
from sklearn.linear_model import LinearRegressionlr = LinearRegression()
lr.fit(X_train, y_train)
pred2 = lr.predict(X_test)
sns.scatterplot(x=y_test, y=pred2)
- 선형 회귀(Linear Regression) 를 사용하여 모델 학습 및 예측 수행.
- 결정 트리와 동일하게 산점도를 활용해 시각화.

모델 성능 평가 (RMSE 계산)
root_mean_squared_error(y_test, pred2)
# DecisionTreeRegressor : 314.3922587940898
# LinearRegression : 420.7751923450068→ 결정 트리 모델이 선형 회귀보다 더 좋은 성능을 보임.
결정 트리 하이퍼파라미터 적용
# 하이퍼파라미터 작용
dtr = DecisionTreeRegressor(random_state=2025, max_depth=50, min_samples_leaf=30)
dtr.fit(X_train, y_train)
pred3 = dtr.predict(X_test)
root_mean_squared_error(y_test, pred3)
# DecisionTreeRegressor : 314.3922587940898
# DecisionTreeRegressor(하이퍼파라미터 적용) : 292.4445072721054
# LinearRegression : 420.7751923450068
- max_depth=50 → 트리의 최대 깊이를 제한하여 과적합 방지.
- min_samples_leaf=30 → 최소 리프 노드 샘플 개수를 30개로 제한.
- RMSE 계산하여 성능 확인.
- → 하이퍼파라미터를 적용한 결정 트리가 기존보다 RMSE가 더 낮아져 성능이 향상됨.
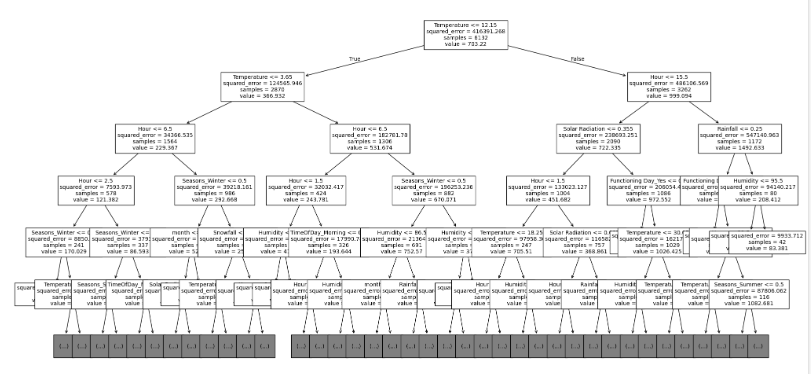
from sklearn.tree import plot_treeplt.figure(figsize=(24, 12))
plot_tree(dtr, max_depth=5, fontsize=10, feature_names=X_train.columns)
plt.show()
- 결정 트리 모델이 학습한 규칙을 트리 형태로 시각화.
- max_depth=5로 설정하여 트리의 깊이를 5까지만 표시 (너무 깊으면 복잡해짐).
- 각 노드에서 MSE(Mean Squared Error)를 최소화하면서 최적의 변수를 찾아 분류.
from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor(random_state=2025)
rf.fit(X_train, y_train)#학습 시키기
pred4 = rf.predict(X_test) #예측하기
root_mean_squared_error(y_test, pred4)#rmse를 구하기
# DecisionTreeRegressor : 314.3922587940898
# DecisionTreeRegressor(하이퍼파라미터 적용) : 292.4445072721054
# RandomForestRegressor : 236.76857513356003
# LinearRegression : 420.7751923450068
- 랜덤 포레스트(Random Forest) 를 사용하여 모델을 학습.
- RMSE를 계산한 결과, 랜덤 포레스트가 가장 낮은 RMSE를 보여 가장 성능이 좋음.
변수 중요도 (Feature Importance) 분석
rf.feature_importances_
# 디시전 트리에서 가중치 중에서 가장 중요하다고 생각하는것을 퍼센트로 알려준것
- 랜덤 포레스트 모델에서 각 특성(Feature)이 예측에 얼마나 중요한지 분석.
- 결과값은 각 변수의 중요도를 퍼센트(%)로 표현.

feature_imp = pd.DataFrame({
'feature':X_train.columns,
'importance':rf.feature_importances_
})feature_imp
top10 = feature_imp.sort_values('importance', ascending=False).head(10)
top10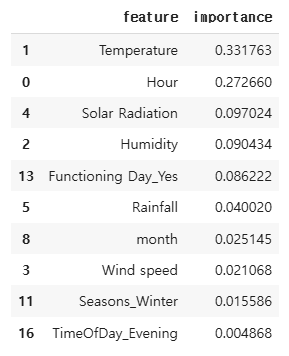
- feature_importances_를 DataFrame으로 변환하여 상위 10개 중요한 변수를 정렬.
plt.figure(figsize=(5, 10))
sns.barplot(x='importance', y='feature', data=top10)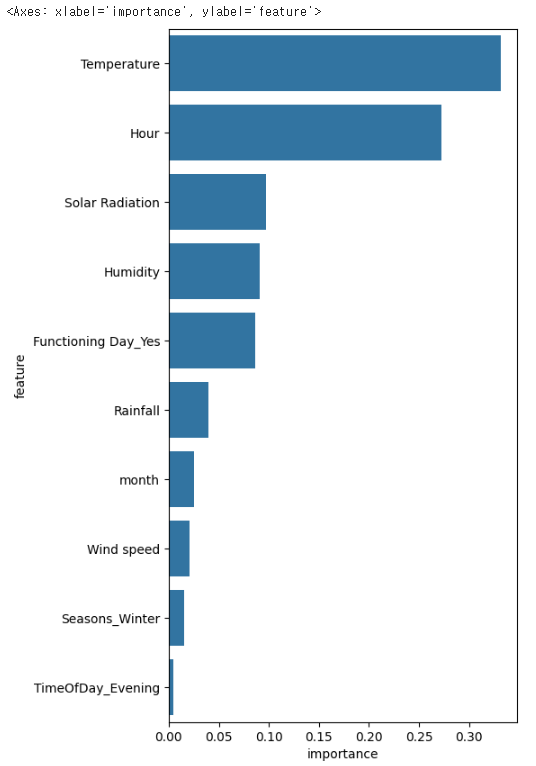
- sns.barplot()을 사용하여 변수 중요도를 막대그래프로 시각화.
- 값이 클수록 모델 예측에 중요한 역할을 함.
그래프 해석
각 변수의 중요도를 보면:
🔹 가장 중요한 변수 TOP 3
- Temperature (기온) → 가장 높은 중요도를 가짐 (~0.33)
- 온도가 높거나 낮을수록 자전거 대여량 변화에 가장 큰 영향을 미침.
- Hour (시간대) → 두 번째로 중요 (~0.27)
- 자전거 대여는 출퇴근 시간(아침, 저녁) 패턴을 강하게 따름.
- Solar Radiation (태양 복사량) → 세 번째로 중요 (~0.12)
- 햇빛이 많을수록 자전거 이용률이 높아지는 경향.
그 외 중요 변수
- Humidity (습도, ~0.10): 습도가 높거나 낮은 날씨가 영향을 미칠 가능성이 있음.
- Functioning Day_Yes (운영 여부, ~0.08): 공휴일이나 특정일에 자전거 대여 여부가 달라질 수 있음.
- Rainfall (강수량, ~0.05): 비가 많이 올수록 자전거 이용량이 줄어듦.
- month (월, ~0.03): 계절에 따른 자전거 사용 패턴을 반영.
- Wind speed (풍속, ~0.02): 바람이 강한 날에는 자전거 이용이 줄어들 가능성이 있음.
- Seasons_Winter (겨울 시즌, ~0.02): 겨울철 자전거 이용 감소를 반영.
- TimeOfDay_Evening (저녁 시간대, ~0.01): 특정 시간대에서 대여량이 변하는 패턴이 있는지 반영.
📌 분석 및 인사이트
✅ Temperature, Hour, Solar Radiation이 가장 중요한 변수임 → 온도와 시간대가 자전거 대여량을 결정하는 가장 중요한 요소!
✅ Rainfall, Wind speed, Seasons_Winter → 날씨 요인이 중요한 역할을 함.
✅ Functioning Day_Yes, month → 운영일 여부와 계절(월별 패턴)이 영향을 미침.
📌 결론
🚴♂️ 자전거 대여량은 Temperature, Hour, Solar Radiation의 영향을 가장 많이 받음
📉 비가 오거나 겨울철에는 대여량이 낮아지는 경향
📊 이 변수들을 활용해 더 정확한 예측 모델을 만들 수 있음!
'인공지능 > 데이터분석' 카테고리의 다른 글
| 슈퍼스토어 마켓팅 캠페인 데이터셋 - Cluster,K-Means (1) | 2025.02.14 |
|---|---|
| 호텔 예약 수요 데이터셋 (0) | 2025.02.02 |
| 주택 임대료 예측 데이터셋 (0) | 2025.01.31 |
| 사이킷런-아이리스(Iris) 데이터셋 분석 (0) | 2025.01.31 |
| 텐서(Tensor) (2) | 2025.01.29 |



